Vector Visualizer
A lean vector algebra and analysis visualization tool written in C++
Goal:
Provide a tool to quickly compute and visualize mathematical vector fields.
Scope:
2-dimensional vector field visualization.
Features:
Define and visualize custom vector fields based on algebraic mathematical expressions.
Define and visualize vector fields based on configurations of point sinks/sources.
Integrate vector fields along custom lines/polygons.
Trace vector field flow lines.
Use cases:
Visualize electrostatic fields by defining configurations of point charges.
Calculate work done when moving around a gravitational field by integrating along custom paths through the field.

The electric field around a positively charged point particle.

The electric field outside a charged spherical shell is equivalent to that of a monopole placed at the center of the ring.

The field around a magnetic dipole.
The electric field inside of a plate capacitor can be assumed to be homogenous as long as the plates of the capacitor are sufficiently long.

The assumption of homogeneity becomes less and less valid as the distance between plates approaches the magnitude of the plate lengths
A spaceship must work when moving further away from a massive object. Conversely, the gravitational field does work on a spaceship as it approaches for a landing.
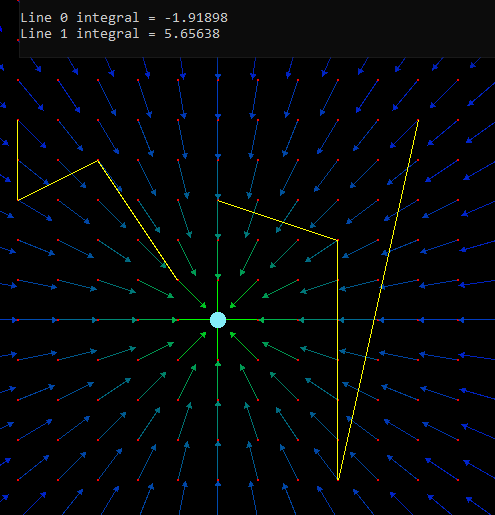
The loop integral vanishes around a monopole. The field is said to be conservative.

The work done when moving in a conservative field is independent of the path taken and only depends on the start and end points of the travelled path.
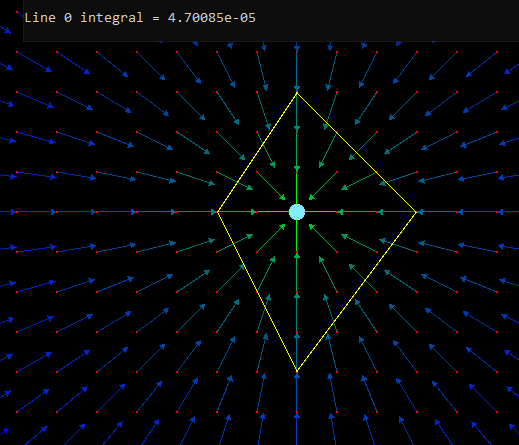
Path independence disappears when a field has a non-zero curl.

Tracing the flow of a non-conservative vector field.